Binary Tree Traversal Code and Upload Your Fillab9zip (Lab9cpp

In this tutorial, you volition learn what a binary search tree is, what parts make upward a tree, and some of the common terms nosotros use when describing parts of a tree.

We will as well see how to traverse a tree using some of the common algorithms – all illustrated with clear examples.

What Is a Binary Search Tree?

A binary search tree is a binary tree made up of nodes. Each node has a central signifying its value.

The value of the nodes on the left subtree are smaller than the value of the root node. And the value of the nodes on the correct subtree are larger than the value of the root node.

The root node is the parent node of both subtrees.

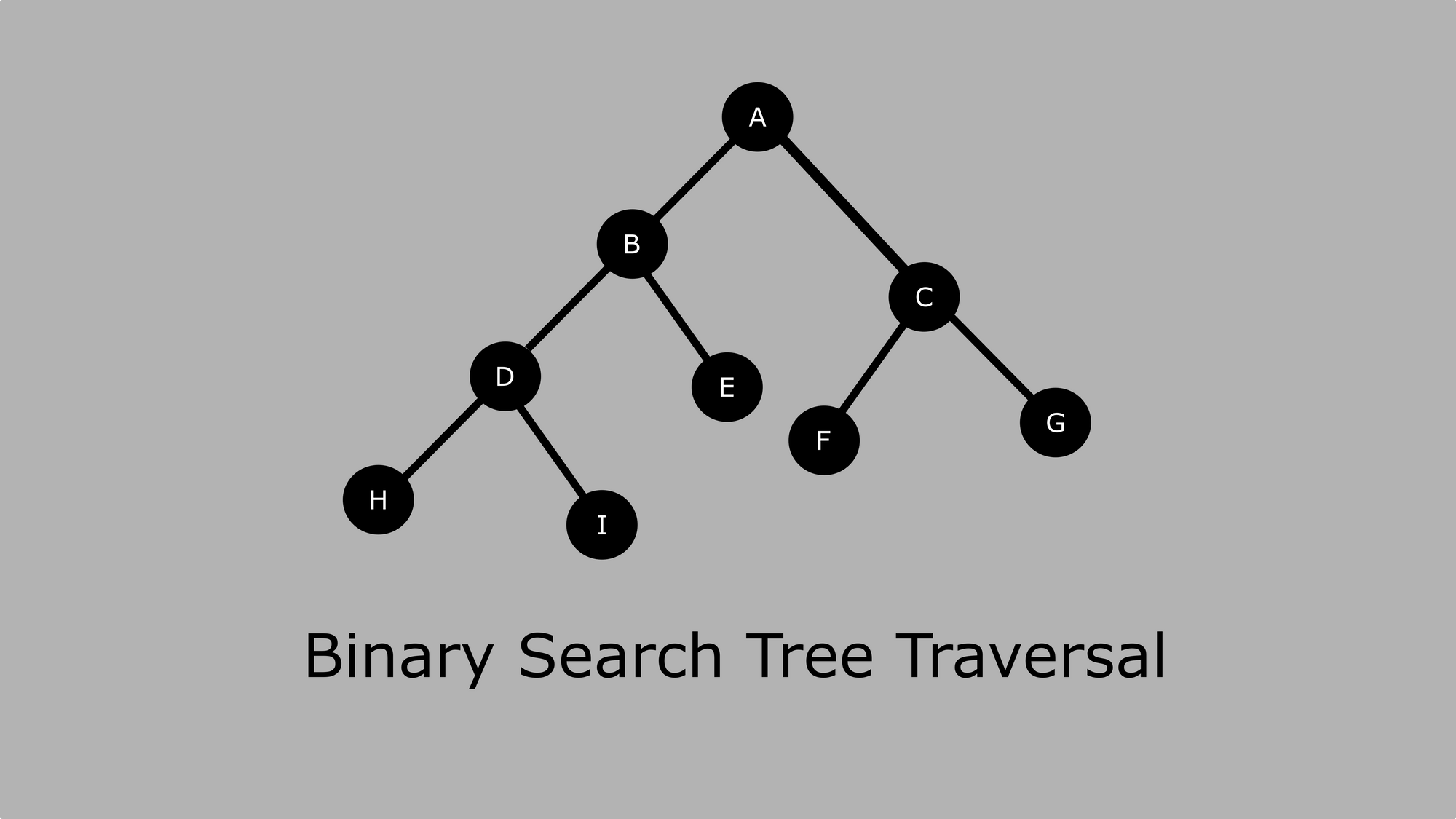
The diagram beneath shows the main parts of a binary tree:

Diagram of a binary search tree

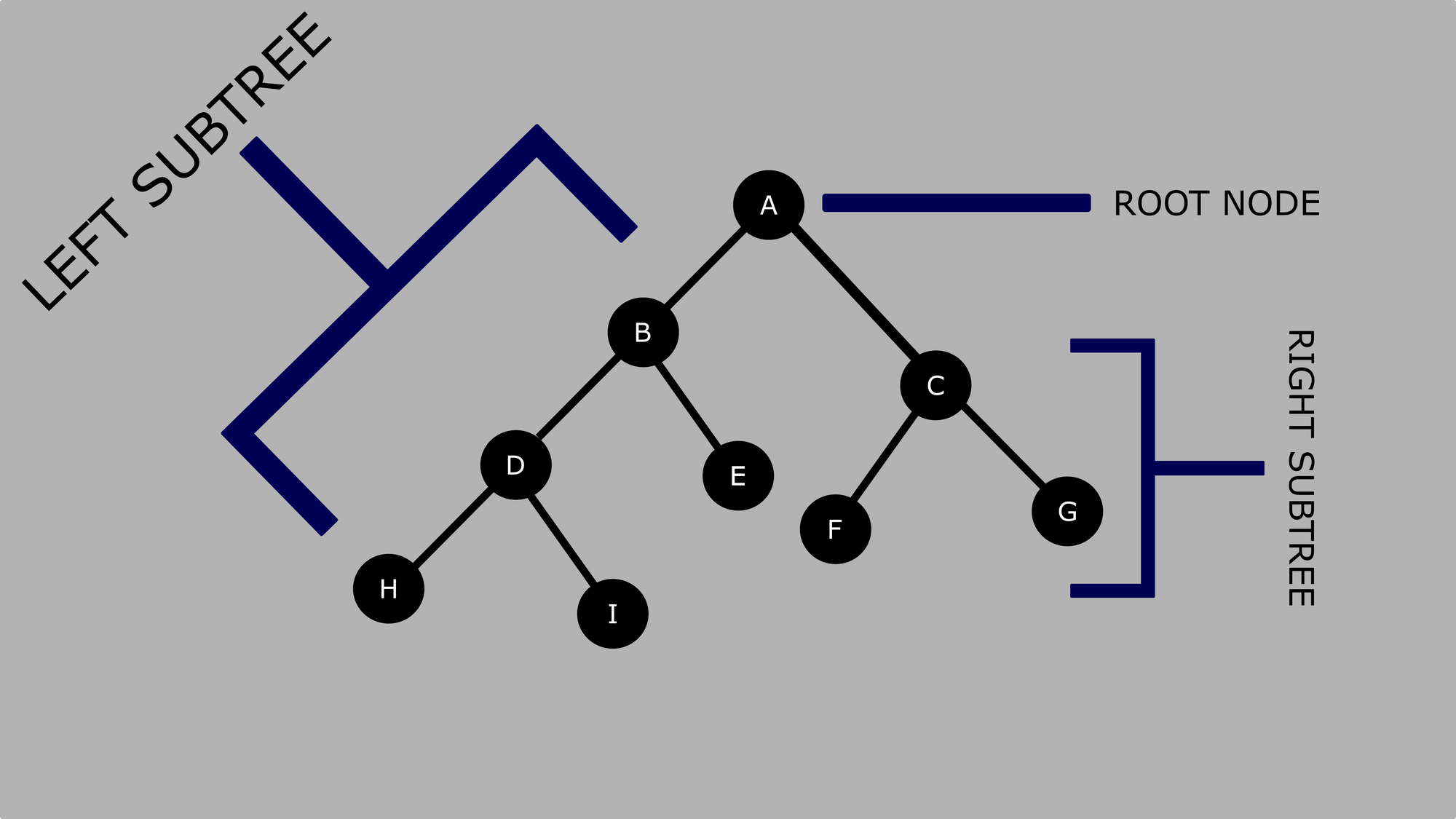
Permit's us look at the relationship between the nodes.

• A is the root node.
• The left subtree begins at B while the right subtree begins at C .
• Node A has two kid nodes – B and C .
• Node C is the parent node to F and G . F and M are siblings.
• Node F and G are know as leafage nodes because they do not have children.
• Node B is the parent node to D and E .
• Node D is the parent node to H and I .
• D and East are siblings as well as H and I .
• Node E is a foliage node.

So here are some important terms that we merely used to describe the tree above:

Root: The topmost node in the tree.

Parent: A node with a kid or children.

Child: A node extended from another node (parent node).

Leaf: A node without a child.

What Is a Binary Search Tree Used For?

Binary search copse assistance the states speed upwardly our binary search as we are able to find items faster.

We can utilise the binary search tree for the improver and deletion of items in a tree.

We tin besides stand for information in a ranked order using a binary tree. And in some cases, it tin be used every bit a chart to correspond a collection of information.

Next, nosotros'll look at some techniques used in traversing a binary tree.

What is Tree Traversal?

Traversing a tree means visiting and outputting the value of each node in a particular gild. In this tutorial, we will use the Inorder, Preorder, and Post order tree traversal methods.

The major importance of tree traversal is that in that location are multiple means of carrying out traversal operations unlike linear information structures like arrays, bitmaps, matrices where traversal is done in a linear order.

Each of these methods of traversing a tree have a particular order they follow:

• For Inorder, you traverse from the left subtree to the root then to the correct subtree.
• For Preorder, you traverse from the root to the left subtree and then to the right subtree.
• For Mail lodge, y'all traverse from the left subtree to the right subtree then to the root.

Here is some other way of representing the data to a higher place:

Inorder => Left, Root, Right.

Preorder => Root, Left, Right.

Mail service lodge => Left, Right, Root.

How to Traverse a Tree Using Inoder Traversal

We are going to create a tree similar to the 1 in the last department, but this time the node keys will be numbers instead of letters.

Recollect that the values of the nodes on the left subtree are e'er smaller than the value of the root node. Also, the values of the nodes on the right subtree are larger than the value of the root node.

Hither is the diagram nosotros volition be working with:

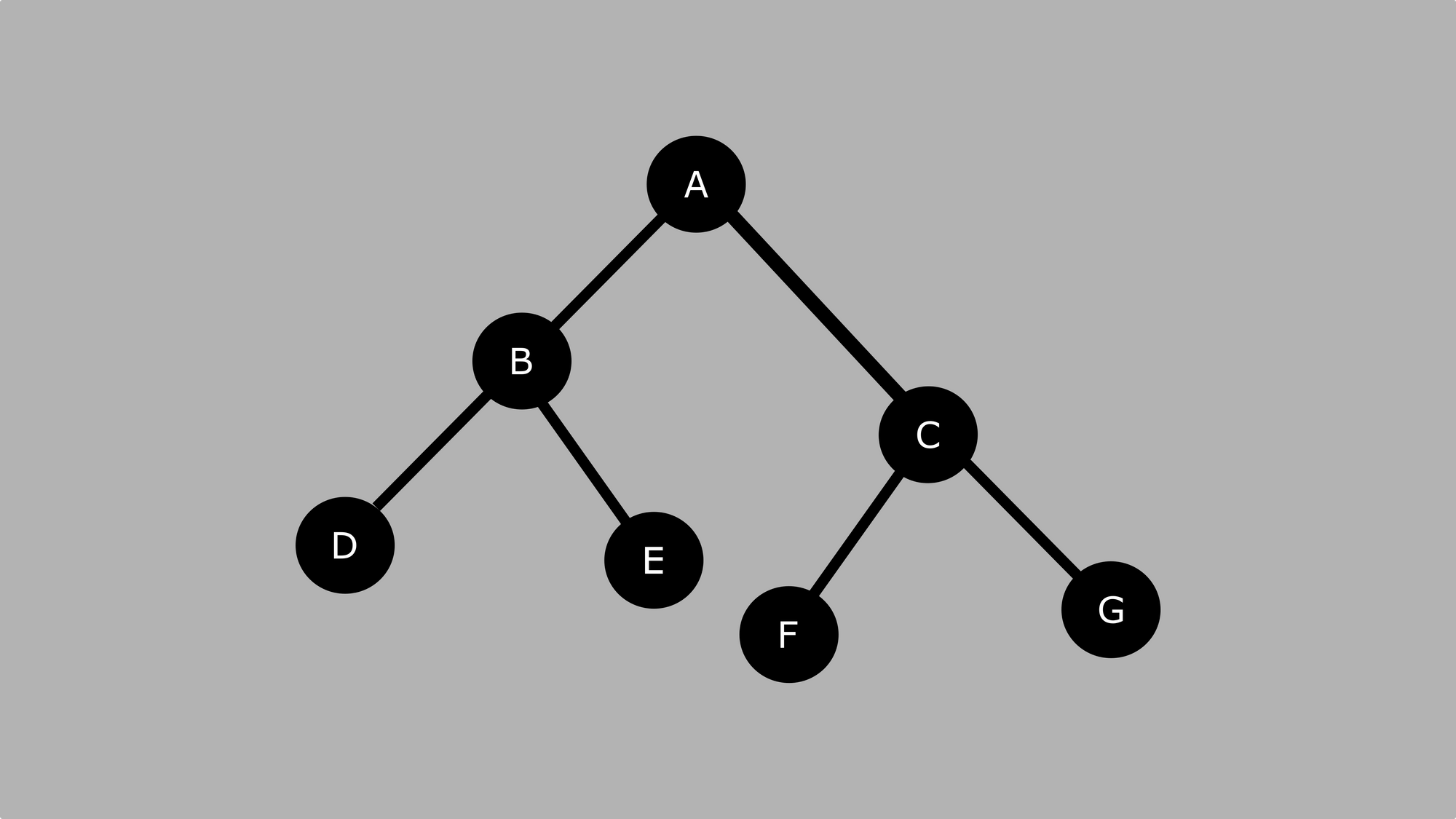
Recollect that the lodge for inorder traversal is Left, Root, Right.

This is the upshot nosotros get later using inorder traversal:

D, B, East, A, F, C, G

If that seems a bit complex for yous to understand, so follow the order of the colors in the pic below

Inorder traversal

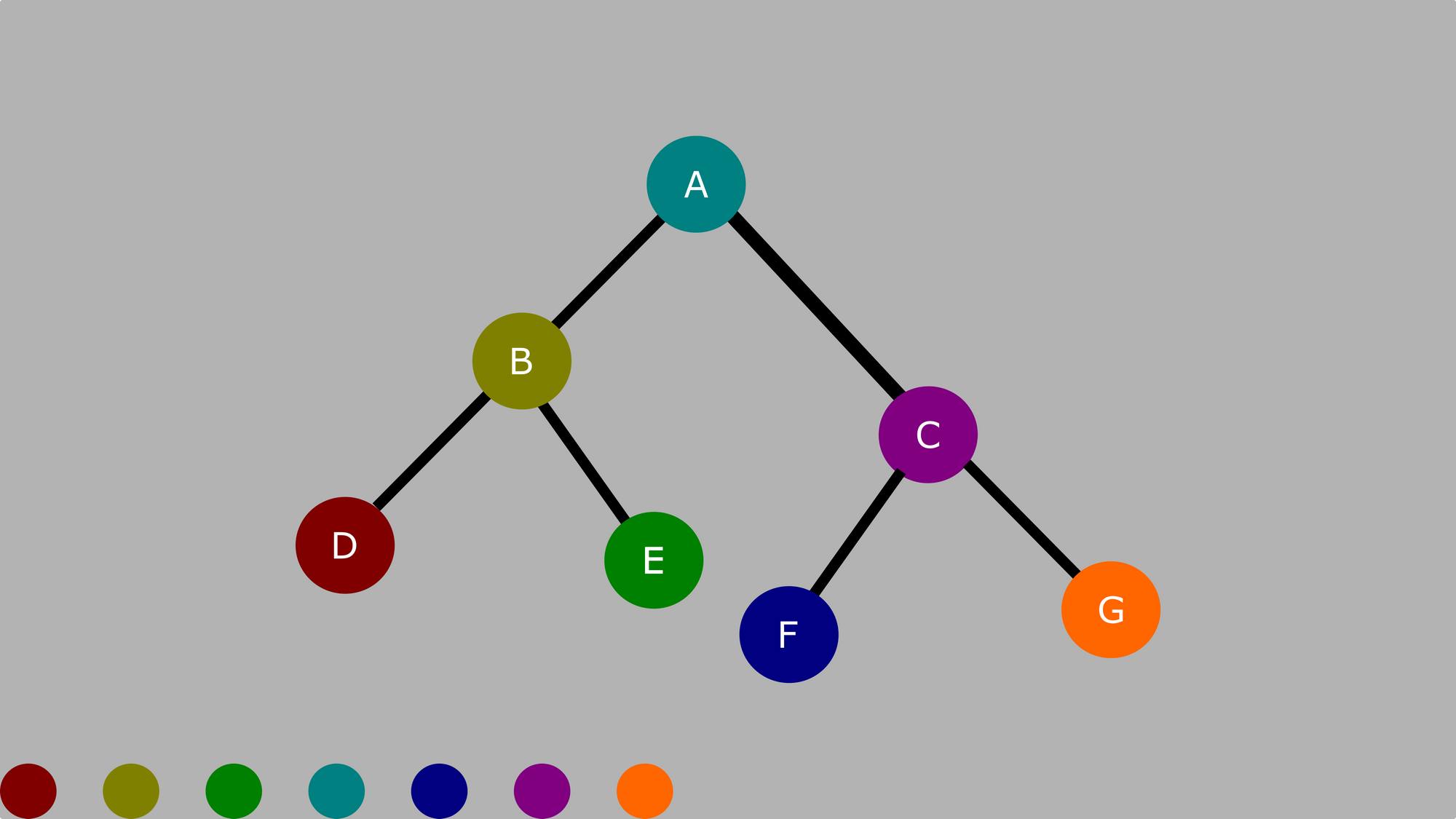
How to Traverse a Tree Using Preorder Traversal

The order here is Root, Left, Right.

Using the aforementioned diagram above, nosotros have:

A, B, D, E, C, F, G

Here is the same diagram with different colors used equally a guide:

Preorder traversal

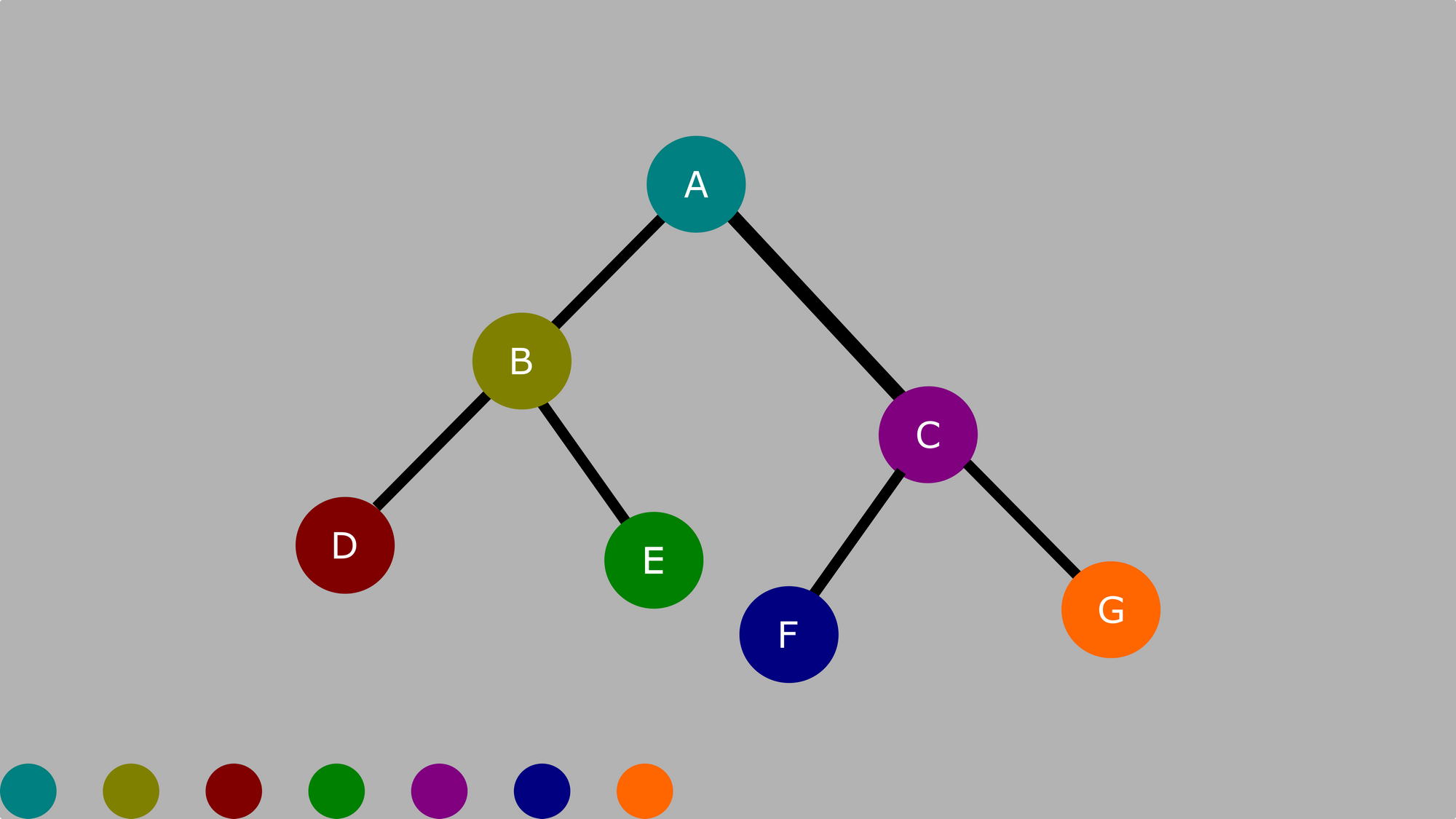
How to Traverse a Tree Using Postorder Traversal

The lodge for postal service order traversal is Left, Right, Root.

Here is the output:

D, Eastward, B, F, One thousand, C, A

If yous can't figure out how we arrived at that consequence, then use the colors in the picture beneath equally a guide:

Postorder traversal

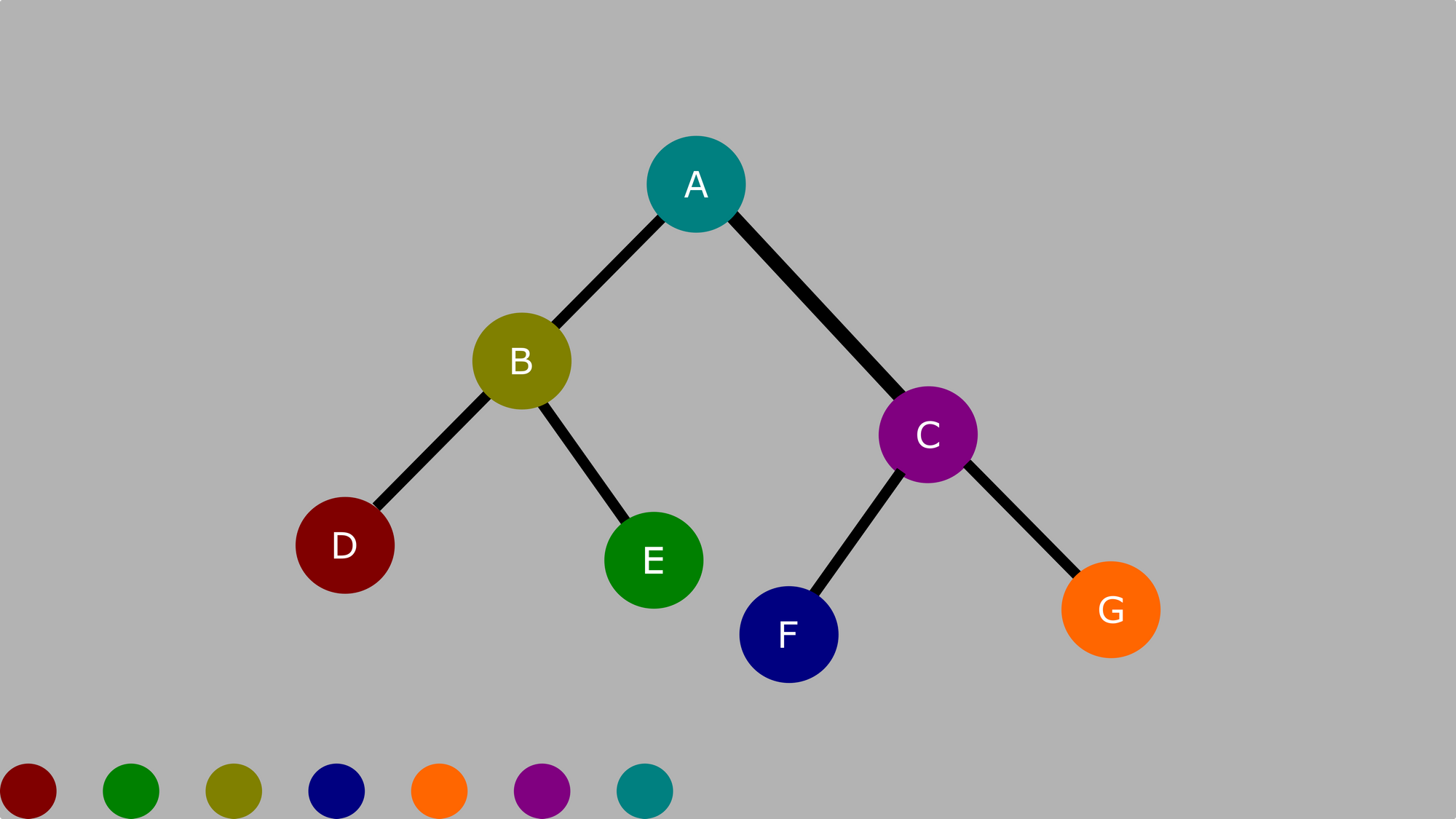
Conclusion

In this tutorial, we learned the basics of what a binary search tree is, what the various parts of a binary tree are, and the common terms associated with a tree. We also saw some of the algorithms nosotros can utilise to traverse a tree.

Thanks for reading!

---

---

Larn to code for free. freeCodeCamp's open source curriculum has helped more than xl,000 people go jobs as developers. Get started

baconnesight1985.blogspot.com

Source: https://www.freecodecamp.org/news/binary-search-tree-traversal-inorder-preorder-post-order-for-bst/

Share this post